const - JS | lectureNumbers, Dates, Intl & Timers

Let's now meet one of the primitive data types we never discussed before, BigInt. BigInt is a special type of integer that was introduced in ES2020 and so let's quickly take a look at it.

In one of the previous lectures, we learned that numbers are represented internally as 64 bits. And that means there are exactly 64 ones or zeros representing any given number.

Now, of these 64 bits, only 53 are actually used to store the digits themselves. The rest are for storing the position of the decimal point and the sign. If there are only 53 bits to store the number, that means that there is a limit of how big numbers can be, and we can calculate that number.

// Biggest number JavaScript can safely represent

console.log(2 ** 53 - 1); // 9007199254740991

We have -1 because numbers start at 0, and 2 because, again, we are working with base 2, which only has zeros and ones. The result of the above calculation is so important that it is stored in the number namespace as a constant called MAX_SAFE_INTEGER.

console.log(Number.MAX_SAFE_INTEGER); // 9007199254740991

So any integer larger than this is not safe, meaning it cannot be represented accurately. Let's have a look at this.

console.log(2 ** 53); // 9007199254740992
console.log(2 ** 53 + 1); // 9007199254740992 (not 9007199254740993)
console.log(2 ** 53 + 0); // 9007199254740992

This clearly shows that JavaScript can simply not represent these numbers accurately. Hence, if we do calculations with numbers that are bigger than Number.MAX_SAFE_INTEGER, then we might lose precision.

It does work with some numbers for some reason, but that's because JavaScript behind the scenes still uses some tricks to represent some of the unsafe numbers. But again, sometimes that works, sometimes it doesn't. And so that's why we call these unsafe numbers.

// Sometimes it works 😁, sometimes it doesn't 😢
console.log(2 ** 53 + 2); // 9007199254740994
console.log(2 ** 53 + 3); // 9007199254740996
console.log(2 ** 53 + 4); // 9007199254740996

You can see that sometimes these numbers look correct and sometimes they don't. And this can be a problem in some situations, we might need really big numbers. Way bigger than Number.MAX_SAFE_INTEGER. For example for database IDs, or when interacting with real 60-bit numbers used in some other programming languages. Hence we might for example from an API receive a number that is bigger than Number.MAX_SAFE_INTEGER. And then we have no way of storing that in JavaScript. At least not until now 😉.

Starting from ES2020, a new primitive was added to JavaScript, called BigInt. BigInt stands for Big Integer, and it can be used to store numbers as large as we want. For example, let's say we have the below number.

console.log(1234567890123456789012345678901234567890);

You can see that when we log the above number, we get in the console a number which probably does not have precision because, of course, it's bigger than Number.MAX_SAFE_INTEGER. But now, if we add the letter n at the end of the number, then we get a BigInt.

console.log(1234567890123456789012345678901234567890n);

The letter n at at the end of the number transforms a regular number into a BigInt. And with that JavaScript can now store and display this number accurately.

We can also create a BigInt from a regular number using the BigInt() function.

/* ⚠️ Without the letter n at the end of the number ⚠️ */
console.log(BigInt(1234567890123456789012345678901234567890));

You will notice that the result is not really the same as the previous one with the letter n at the end of the number. My guess is that JavaScript still needs to represent the number internally, before it can then convert it to a BigInt.

Now that we know how to create a BigInt number, let's now see some operations we can do with it. All the usual operators still work the same. Let's have some examples.

console.log('BIGINT ADDITION');
console.log(15000n + 15000n);

console.log('BIGINT MULTIPLICATION');
console.log(549798792398984961799853338181482n * 6000000n);

What's not possible with BigInts is to mix them with regular numbers. For example, if we try to add a regular number to a BigInt, then we get an error.

console.log('BIGINT ADDITION WITH REGULAR NUMBER');
const huge = 985447812345678901234567890n;
const num = 23;
console.log(huge + num);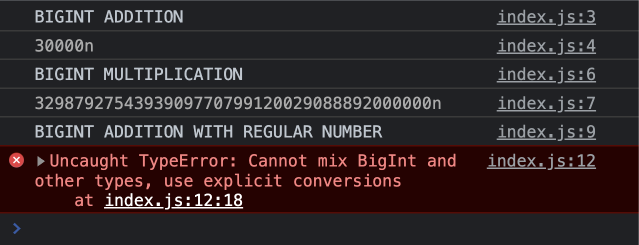

To fix this, all we have to do is the convert the regular number to a BigInt using the constructor function.

console.log(huge + BigInt(num)); // 👌🏽

However, there are two exceptions to this: the comparison operators and the plus operator when working with strings. Let's see some examples.

console.log(20n > 15); // true

This works as expected. However, the below does not.

console.log(20n === 20); // false

This actually makes sense because, when we use the triple operator in JavaScript, it does not do type coercion. And in fact 20n and 20 are two different primitive types.

console.log(typeof 20n); // bigint
console.log(typeof 20); // number

However, if we use the regular equality operator (loose equality), then JavaScript will do type coercion and convert the BigInt to a regular number.

console.log(20n == 20); // true
console.log(20n == '20'); // true

The other exception as mentionned above is when we use the plus operator with strings during concatenations.

console.log('The amount raised by this company was: ' + 9000000000000n);

Next, the Math operations we saw in one of the previous lectures, do not work with BigInts. For example, if we try to use Math.sqrt() with a BigInt, then we get an error.

console.log(Math.sqrt(16n)); // Error

Finally, let's take a look at what happens with divisions

console.log(10n / 3n); // 3n
console.log(10 / 3); // 3.3333333...

With BigInt, JavaScript will simply return the closest BigInt, and cuts off the decimal part.